Streaming vs Batch: A Case Study with Longest Consecutive Sequence
When Union-Find beats HashSet and why access patterns determine algorithm choice
The classic LeetCode 128 problem asks for the longest consecutive sequence in an unsorted array. The standard O(n) solution uses a HashSet - but what if your data arrives incrementally?
The Standard Solution
The textbook approach builds a set, then for each potential sequence start (no predecessor exists), counts upward:
int longestConsecutive(vector<int>& nums) {
unordered_set<int> s(nums.begin(), nums.end());
int longest = 0;
for (int n : s) {
if (s.find(n - 1) == s.end()) { // sequence start
int len = 1;
while (s.find(n + len) != s.end()) len++;
longest = max(longest, len);
}
}
return longest;
}O(n) time, O(n) space. Each element visited at most twice.
The Streaming Variant
If data arrives incrementally and you need answers during ingestion, rebuilding the set each time gives O(n²) total work.
The natural solution is Union-Find (disjoint set union) - a standard data structure for incremental connectivity problems. Each number joins or merges clusters with its neighbors:
void addElement(int item) {
if (seen(item)) return;
bool has_left = seen(item - 1);
bool has_right = seen(item + 1);
if (has_left && has_right) {
merge(cluster(item-1), cluster(item+1));Show all 17 lines
void addElement(int item) {
if (seen(item)) return;
bool has_left = seen(item - 1);
bool has_right = seen(item + 1);
if (has_left && has_right) {
merge(cluster(item-1), cluster(item+1));
assign(item, cluster(item-1));
} else if (has_left) {
assign(item, cluster(item-1));
} else if (has_right) {
assign(item, cluster(item+1));
} else {
create_new_cluster(item);
}
}With path compression and union by size, each operation is O(α(n)) amortized, where α is the inverse Ackermann function - effectively constant for all practical inputs.
The Tradeoff
Both approaches are O(n) for processing n elements once. But:
- HashSet: 1 data structure, cache-friendly iteration, simple
- Union-Find: 3 hash maps (parent, items, counts), more pointer chasing
For a single batch query, the constant factors favor HashSet:
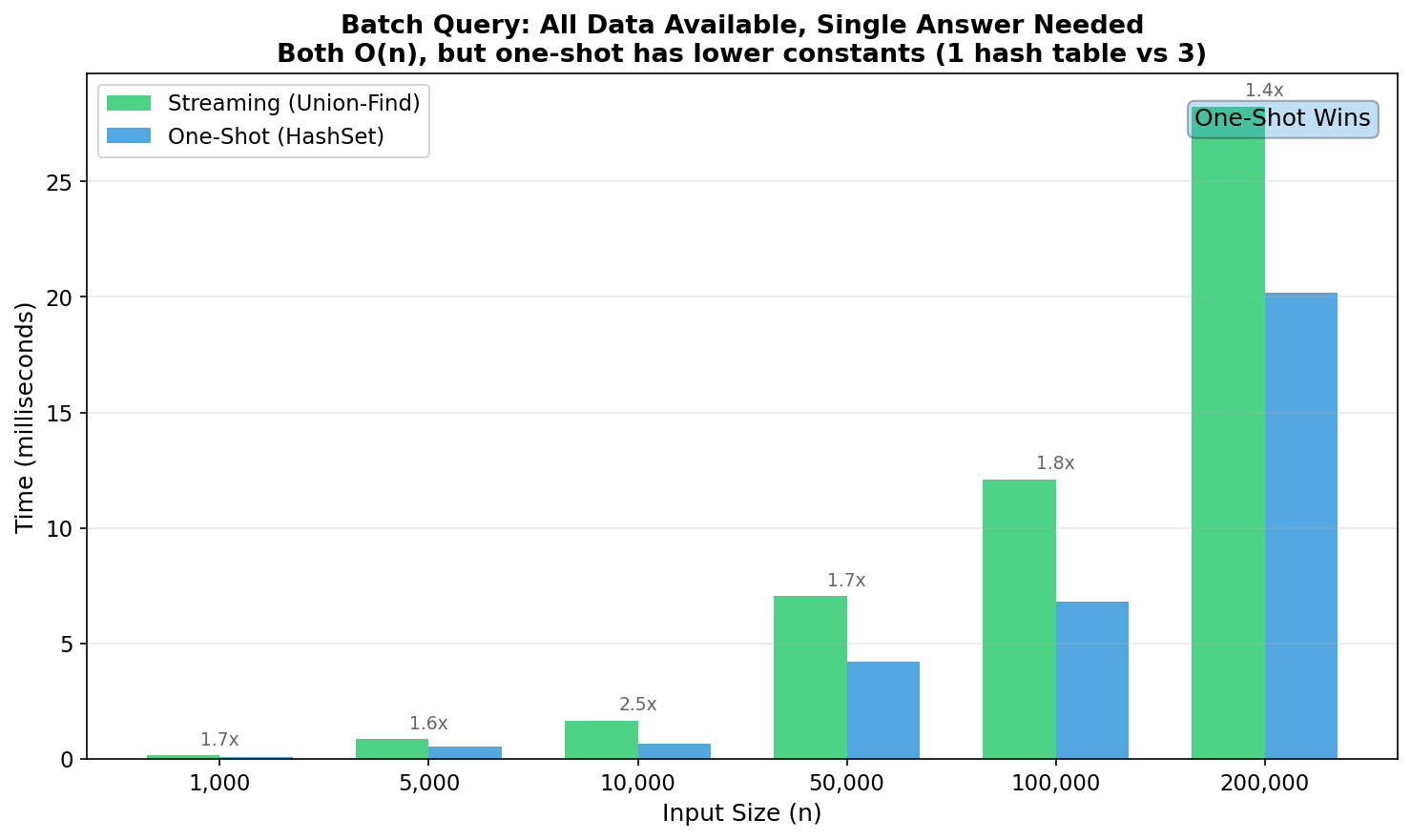
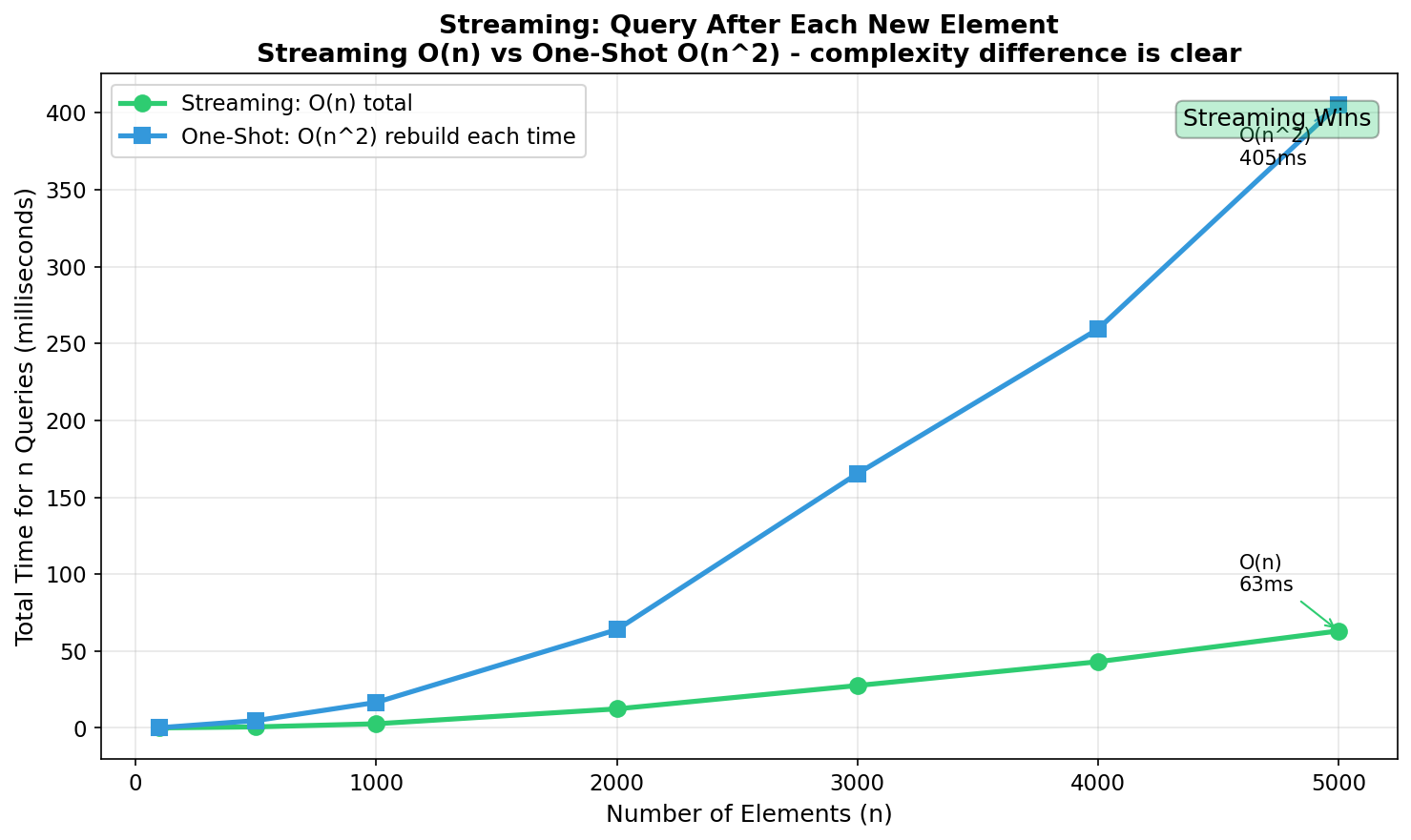
But for incremental queries - where you need the answer after each insertion - the complexity changes fundamentally:
- Streaming (Union-Find): O(n) total for n inserts + n queries
- Batch (HashSet): O(n²) - rebuild O(n) structure n times
When to Use Which
| Access Pattern | Algorithm | Why |
|---|---|---|
| All data upfront, single query | HashSet | Lower constants, simpler |
| Incremental data, periodic queries | Union-Find | Amortized incremental updates |
| Mixed (mostly batch, rare updates) | HashSet + invalidation | Rebuild only when needed |
This is a standard batch-vs-streaming tradeoff that appears throughout systems design - from database indexing strategies to cache invalidation policies. The lesson isn't about this specific problem, but about matching algorithm choice to access patterns.
Complexity Notes
Real-world performance depends on:
- Hash table implementation and load factors
- Cache behavior (sequential vs random access)
- Data distribution (duplicates, clustering)
The benchmarks above use random data with ~10% duplicates. Your mileage will vary - profile with representative data before committing to an approach.
Benchmark Environment
- Hardware: MacBook Air, Apple M4 (10-core: 4P + 6E), 24GB RAM
- Compiler: Apple clang 17.0.0,
-std=c++17 -O3
Full Implementation
#include <iostream>
#include <vector>
#include <string>
#include <unordered_map>
#include <algorithm>
#include <functional>
class Solution {Show all 85 lines
#include <iostream>
#include <vector>
#include <string>
#include <unordered_map>
#include <algorithm>
#include <functional>
class Solution {
public:
int longestConsecutive(std::vector<int>& nums) {
using ClusterId = int;
std::unordered_map<int, ClusterId> item_to_cluster;
std::unordered_map<ClusterId, ClusterId> parent;
std::unordered_map<ClusterId, std::size_t> cluster_size;
ClusterId next_cluster_id = 0;
auto has = [](const auto& map, auto key) {
return map.find(key) != map.end();
};
// Union-Find: find with path compression - O(α(n)) amortized
std::function<ClusterId(ClusterId)> find = [&](ClusterId id) -> ClusterId {
if (!has(parent, id)) parent[id] = id;
if (parent[id] != id) {
parent[id] = find(parent[id]);
}
return parent[id];
};
// Union-Find: union by size - O(α(n)) amortized
auto merge = [&](ClusterId a, ClusterId b) -> ClusterId {
ClusterId root_a = find(a);
ClusterId root_b = find(b);
if (root_a == root_b) return root_a;
if (cluster_size[root_a] >= cluster_size[root_b]) {
parent[root_b] = root_a;
cluster_size[root_a] += cluster_size[root_b];
return root_a;
}
parent[root_a] = root_b;
cluster_size[root_b] += cluster_size[root_a];
return root_b;
};
for (int item : nums) {
if (has(item_to_cluster, item)) continue;
bool has_left = has(item_to_cluster, item - 1);
bool has_right = has(item_to_cluster, item + 1);
if (has_left && has_right) {
ClusterId left_root = find(item_to_cluster[item - 1]);
ClusterId right_root = find(item_to_cluster[item + 1]);
ClusterId merged = merge(left_root, right_root);
item_to_cluster[item] = merged;
cluster_size[merged]++;
} else if (has_left) {
ClusterId root = find(item_to_cluster[item - 1]);
item_to_cluster[item] = root;
cluster_size[root]++;
} else if (has_right) {
ClusterId root = find(item_to_cluster[item + 1]);
item_to_cluster[item] = root;
cluster_size[root]++;
} else {
item_to_cluster[item] = next_cluster_id;
cluster_size[next_cluster_id] = 1;
next_cluster_id++;
}
}
std::size_t max_size = 0;
for (const auto& [cluster_id, size] : cluster_size) {
if (find(cluster_id) == cluster_id) {
max_size = std::max(max_size, size);
}
}
return static_cast<int>(max_size);
}
};